Penyederhanaan Fungsi Boolean Dengan Karnaugh Map

Setelah cukup memahami teorema aljabar Boolean, penyederhanaan fungsi Boolean dengan aljabar, dan model-model Karnaugh Map beserta pemetaannya, kini saatnya mencoba menyelesaikan fungsi logika Boolean dengan Peta Karnaugh (Karnaugh Map/ K-Map). Jika suatu fungsi logika memiliki tiga atau empat variabel, maka penyelesaian dengan K-Map ini akan lebih mudah dibanding dengan penyederhanaan cara Aljabar.

Dari beberapa model K-Map yang telah dibahas sebelumnya, penyederhanaan fungsi logika pada posting ini hanya akan menggunakan model-1 karena metode penyederhanaan dengan model-model K-Map lain pun hasilnya akan tetap sama.

PENYEDERHANAAN DUA VARIABEL
Contoh 1.
F = AB + A'B + AB'

Penyelesaian:

1. Gambarkan K-Map Model-1 untuk dua variabel
2. Ganti kotak-kotak yang sesuai untuk AB, A'B, dan AB, dengan angka satu (1) dan sisanya dengan angka nol (0)
   
   
   
   
3. Gabungkan semua angka satu (1) sesederhana mungkin. Untuk mempermudah dapat menggunakan pemetaan K-Map dua variabel.
   
   
   
   
4. Hasil penyederhanaan dari F = AB + A'B + AB' adalah F = A + B

Perbandingan dengan cara Aljabar:
F = AB + A'B + AB'
   = A (B+B') + A'B
   = A (1) + A'B
   = A + A'B
   = A + B (Teorema T9)

Perbandingan dengan software Karnaugh Map Explorer 1.0

Contoh 2.
F = AB' + A'B'

Penyelesaian:

1. Gambarkan K-Map Model-1 untuk dua variabel
2. Ganti kotak-kotak yang sesuai untuk AB' dan A'B' dengan angka satu (1) dan sisanya dengan angka nol (0)
   
   
   
   
3. Gabungkan semua angka satu (1) sesederhana mungkin. Untuk mempermudah dapat menggunakan pemetaan K-Map dua variabel.
   
   
   
   
4. Hasil penyederhanaan adalah F = B'

Perbandingan dengan cara Aljabar:
F = AB' + A'B'
   = (A+A') B'
   = (1) B'
   = B'

Perbandingan dengan software Karnaugh Map Explorer 1.0

PENYEDERHANAAN TIGA VARIABEL
Contoh 1.
F = ABC' + AB'C' + AB'C + ABC

Penyelesaian:

1. Gambarkan K-Map Model-1 untuk 3 variabel kemudian tandai dengan angka satu (1) setiap kotak yang mewakili ABC', AB'C', AB'C, dan ABC, sisanya diisi dengan angka nol (0).
   
   
   
   
2. Gambarkan pemetaan K-Map untuk 3 variabel yang paling mendekati dan paling sederhana. Pada kasus ini area A pada K-Map dapat mewakili semua variabel dalam soal.
   
   
   
   
3. Hasil penyederhanaan dari F = ABC' + AB'C' + AB'C + ABC adalah F = A

Perbandingan dengan Aljabar:
F = ABC' + AB'C' + AB'C + ABC
   = AB (C'+C) + AB' (C'+C)
   = AB (1) + AB' (1)
   = AB + AB'
   = A (B+B')
   = A (1)
   = A

Perbandingan dengan software Karnaugh Map Explorer 1.0

Contoh 2.
F = A'B'C + A'BC + AB'C + ABC + ABC'

Penyelsesaian

1. Gambarkan K-Map Model-1 untuk 3 variabel kemudian tandai dengan angka satu (1) setiap kotak yang mewakili A'B'C, A'BC, AB'C, dan ABC, dan ABC', sisanya diisi dengan angka nol (0).
   
   
   
   
2. Gambarkan pemetaan K-Map untuk 3 variabel yang paling mendekati dan paling sederhana. Pada kasus ini area AB dan area C pada K-Map dapat mewakili semua variabel dalam soal.
   
   
   
   
   
3. Penyederhanaan dari F = A'B'C + A'BC + AB'C + ABC + ABC' adalah F = AB + C

Perbandingan dengan Aljabar:
F = A'B'C + A'BC + AB'C + ABC + ABC'
   = (A'+A)B'C + (A'+A)BC + ABC'
   = (1) B'C + (1) BC + ABC'
   = B'C + BC + ABC'
   = (B'+B)C + ABC'
   = (1) C + ABC'
   = C + ABC'
   = C + AB (Teorema T9)
   = AB + C

Perbandingan dengan software Karnaugh Map Explorer 1.0

PENYEDERHANAAN EMPAT VARIABEL
F = A'BC'D + ABC'D + A'BCD + ABCD

Penyelsesaian

1. Gambarkan K-Map Model-1 untuk 4 variabel kemudian tandai dengan angka satu (1) setiap kotak yang mewakili A'BC'D, ABC'D, A'BCD, ABCD, sisanya diisi dengan angka nol (0).
   
   
   
   
2. Gambarkan pemetaan K-Map untuk 4 variabel yang paling mendekati dan paling sederhana. Pada kasus ini area B dab D pada K-Map dapat mewakili semua variabel dalam soal.
   
   
   
   
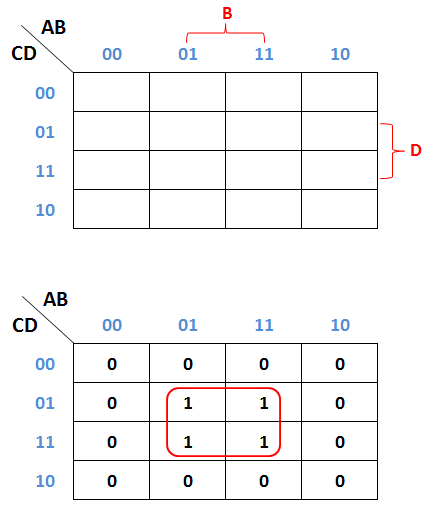
3. Hasil penyederhanaan dari F = A'BC'D + ABC'D + A'BCD + ABCD adalah F = BD

Perbandingan dengan Aljabar:
F = A'BC'D + ABC'D + A'BCD + ABCD
   = (A'+A) BC'D + (A'+A) BCD
   = (1) BC'D + (1) BCD
   = BC'D + BCD
   = BD (C'+C)
   = BD (1)
   = BD

Perbandingan dengan software Karnaugh Map Explorer 1.0